Introduction

This post talks about a lexer I made a couple of years ago and remember fondly, it has brief sections about lexers in general, the idea I had of a lexer and how I implemented it. You can found the repository here although it has been created and updated later than that .

Lexers

A lexical analizer (or lexer) is a program that reads some input (the source code of a program) and generates a symbol or token table a parser will later use as input.

More formally, the Dragon Book defines the function of a lexer as:

… the first phase of a compiler, the main task of the lexical analyzer is to read the input characters of the source program, group them into lexemes, and produce as output a sequence of tokens for each lexeme in the source program.

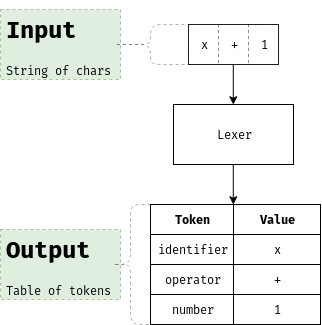
The basic functionality of a lexer is represented on the image bellow:

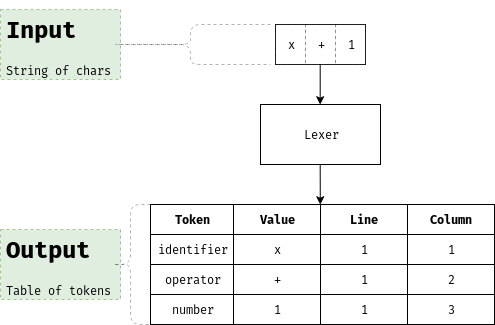
However, knowing where a symbol (or token) is located within the input data can be really useful in error reporting and later steps, so our process will be more similar to this representation:

What was that about automatons

But don’t lexers usually use (usually) non-deterministic automatons in the form of regular expressions to categorize the lexemes?

Absolutely yes, and many of those lexers are not only cleverly implemented but also field-tested. However we are here for the fun of building something despite the existence of a much better alternative and never using it again.

That said, there are some main differences I would like to express:

• The automaton being deterministic means the analyzer will never have to choose between two valid token types.
• When defining the lexemes we will not focus on the characters they may have, rather in the valid transitions between a character of the lexeme and the next.

Definition of the automatons

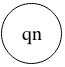
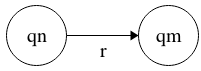
Representation

State qn

where n is the number of the state. The initial state will always be q0. If the automaton stops at a non-final state, the symbol will not be recognized.

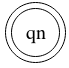
Final state qn

same as a normal state but with an inner circle. The final state of the automaton when processing a symbol will determine it’s type.

Transition r

where r is a regular expression contemplating a single character. Transitions go from one state to another or to the same state (a loop). Two transitions from the same node can never satisfy the regular expression simultaneously.

Considerations

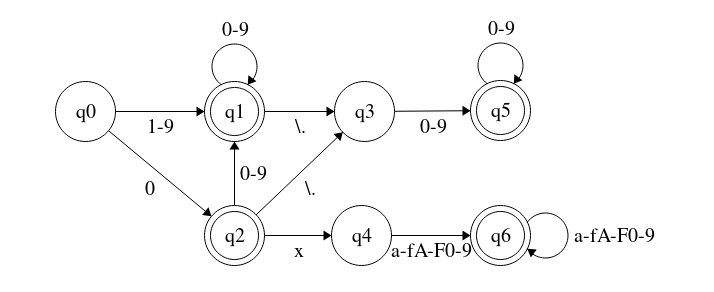
• To ensure the determinism of the automaton we need to merge the automaton of each lexeme into a single automaton every lexemization will start from. E.g. if we want to be able to have numbers (explained later in this page) and hexadecimal numbers, we will need to merge this two automatons:

into another automaton compatible with the previous ones:

Examples

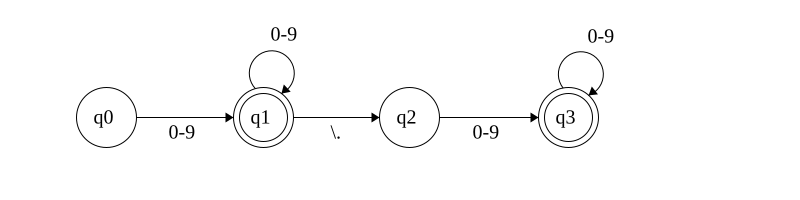
Number

A number (with or without decimal notation) can be defined with the regular expression:

^[0-9]+(\.[0-9]+)?$

In our case we will need a deterministic finite automaton like the following:

If we fed the automaton a string such as 42 or 5.05 it would stop at the second but would reject others such as a1, .1 or 1.a.

You might have realized it would accept 1a and 1.1a, that is because I’ve arbitrarily decided that 1.1a is actually the number 1.1 followed by the identifier a and it’s up to the parser to decide whether or not that is allowed. In both 1a and 1.1a the automaton would only accept the number part and the automaton representing identifiers would have to accept the rest.

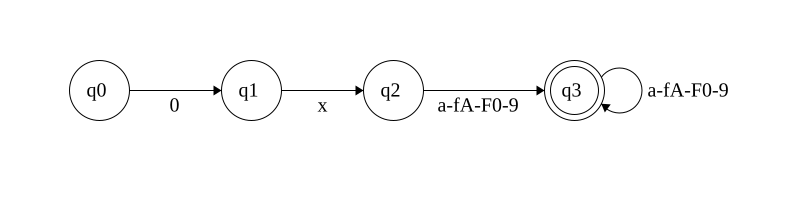
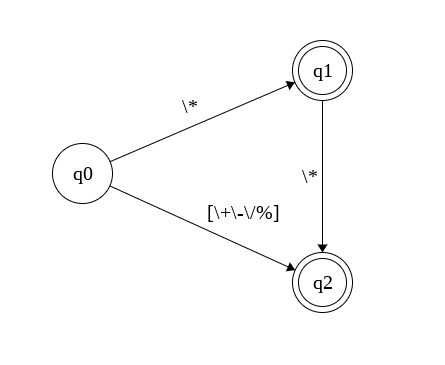
Operators

Let’s suppose our language will support the operators +, -, *, **, / and %. Then our regular expression would be:

^(\+|\-|(\*[\*]?)|\/|%)$

The corresponding automaton looks like:

This one is a bit more straightforward, if the character is +, -, / or % it is immediately accepted as an operator, if it’s * it is either followed by another * and accepted or followed by anything else and also accepted.

Hands on

Quick note: from now on we will be referring to states as nodes, transitions as paths and symbols as tokens.

Algorithm

After building the automaton the algorithm is simple:

1. current_char := fist_char()
2. current_node := q0
3. Look for a valid path for current_char from current_node:
     If a path is found:
       current_node = path.target; current_char = next_char(); goto 3
     If no path is found and the node is final:
       store $current_node.symbol; goto 2
     If no path is found and the node is not final:
       error: unrecognized symbol; exit

Complexity

Each character is only processed once (or twice in the case of final characters) making the complexity approximately O(n×m) where:

• n is the number of characters in the input file
• m is the number of paths in the node

If that complexity scares us, we can lie to ourselves simplify it by supposing that m will be a very small number in best and average cases, living us with a much prettier O(n×k) → O(n) in best and average cases and O(n×m) in worst cases. We can now show off our algorithm while hiding our shame.

Coding

The language chosen for this example is Go for three reasons: readability, Go being the language I was learning at the time and the joy the gopher brings me.

Automaton types

Token

A token is a just string with the name of the type of token (number, operator, identifier…). token.go:

// Token represents a type of token of the language
type Token string

Node

A node contains a list of paths to other nodes, wether it is a final node and if so what token type it represents. node.go:

// Node represents a state of the automaton
type Node struct {
    Final bool
    Paths []Path
    Token Token
}

Path

A path has a regular expression as the condition for transiting and a target node. path.go:

import re "regexp"

// Path connects to a node over a regular expression
type Path struct {
    Exp    re.Regexp // regular expression used as transition condition
    Target *Node     // target node
}

Building the automaton

To make things easier, the automaton can be serialized to/read from a JSON. The JSON has the following structure:

{
  "tokens": [
    "assignator",
    "binary-operator",
    ...
    "whitespace"
  ],
  "nodes": {
    "q0": {
      "final": false,
      "paths": {
        "<regex>": "<target>",
      }
    },
    ...,
    "qn": {...}
  }
}

Where tokens contains all the types of Tokens and nodes the full list of nodes (states) and paths (transition) of the automaton.

The unmarshalling the JSON is not part of the post, but if you are interested you can take a look at the file I made for it.

A full definition of the automatons made for the project can be found at my bitbucket wiki and the JSON representation of those at the corresponding file.

Lexer

A Lexer struct will come handy when tokenizing the source. lexer.go:

// Lexer is used to build and store the token table
type Lexer struct {
    ahead       int          // peek level
    buffer      bytes.Buffer // buffer stores the chars of the current token
    currentChar byte         // value of the current char
    position    position     // position of the current token
    source      []byte       // source contains the source file content
    tokenizer   Tokenizer    // struct built with utils for actions
                             //  such as unmarshalling the automaton
}

type position struct {
    column int // relative position of the char in the current line
    index  int // absolute position of the char
    line   int // line of the char
}

Token table

I swear this is the last one before the algorithm . A token table will store the tokens the lexer has been producing. tokentable.go:

// TokenTable stores information about tokens generated by Lexer
type TokenTable struct {
    Tokens   []Token   // type of token
    Values   []string  // value of the token
    Lines    []uint    // line the token is located at
    LinePosI []uint    // initial column of the token
    LinePosE []uint    // end column of the token
}

// writeToken inserts a token into the token table
func (tt *TokenTable) writeToken(t Token, v string, l uint, posi uint, pose uint) {
    tt.Tokens = append(tt.Tokens, t)
    tt.Values = append(tt.Values, v)
    tt.Lines = append(tt.Lines, l)
    tt.LinePosI = append(tt.LinePosI, posi)
    tt.LinePosE = append(tt.LinePosE, pose)
}

Finally, the algorithm

The day has come! If any one has made it this far thank you for your time! Hope it wasn’t too bad…

The last part is to code the algorithm described in a previous part.

First we create a function to generate a single token:

// tokenize a single token
func (l *Lexer) tokenize(node *Node, tt *TokenTable) (bool, error) {
    // if l.currentChar matches a pattern, follow corresponding path
    for _, path := range node.Paths {
        if path.Exp.MatchString(string(l.currentChar)) {
            l.buffer.WriteByte(l.currentChar)

            // if it's the last character
            if l.position.index+l.ahead+1 >= len(l.source) {
                if path.Target.Final {
                    l.writeToken(path.Target.Token, tt)
                    return true, nil
                }
            }
            // if it's not the last character
            l.peek(1)
            return l.tokenize(path.Target, tt)
        }
    }
    // if current state is a final state, return token & consume
    if node.Final {
        l.writeToken(node.Token, tt)
        l.consume(l.ahead)
        return false, nil
    }
    // if state is not final and there are no valid paths, unrecognized token
    return true, fmt.Errorf("unrecognized token '%v' (line %d, column %d)",
        l.buffer.String(), l.position.line, l.position.column)
}

And later to tokenize a whole file passed (arbitrarily, mostly for flexibility ) as an io.Reader:

// Tokenize tokenizes all the input in the io.Reader
func (l *Lexer) Tokenize(in io.Reader) (*TokenTable, error) {
    // read the content of the source file
    source, err := ioutil.ReadAll(in)
    if err != nil {
        return nil, err
    }

    // create the token table, initialize the structs
    tokenTable := &TokenTable{}
    l.source = source
    l.nextChar()

    // q0 is the initial token
    l.tokenize(l.tokenizer.Nodes["q0"], tokenTable)

    // tokenize returns end if the analyzed element was the last element
    for l.position.index < len(l.source) {
        end, err := l.tokenize(l.tokenizer.Nodes["q0"], tokenTable)
        if err != nil {
            return nil, err
        }
        if end {
            break
        }
    }
    return tokenTable, nil
}

Running the code

We are almost done but we need a runnable file! It just needs to get an input file and the definition of the automaton. I’ll be using the one at the repository.

The test source file test.source:

y = x + 1
"hello"

After some prettyprinting, running the file outputs:

$ go run main.go -source test.source -rules <path-to-automaton>

+------------------+---------+------+--------------+------------+                     
|      TOKEN       |  VALUE  | LINE | START COLUMN | END COLUMN |                     
+------------------+---------+------+--------------+------------+                     
| identifier       | y       | 1    | 1            | 2          |                     
| whitespace       |         | 1    | 2            | 3          |                     
| assignator       | =       | 1    | 3            | 4          |                     
| whitespace       |         | 1    | 4            | 5          |                     
| identifier       | x       | 1    | 5            | 6          |                     
| whitespace       |         | 1    | 6            | 7          |                     
| operator         | +       | 1    | 7            | 8          |                     
| whitespace       |         | 1    | 8            | 9          |                     
| number           | 1       | 1    | 9            | 10         |                     
| end-of-statement | \n      | 1    | 10           | 11         |                     
| string           | "hello" | 2    | 1            | 8          |                     
| end-of-statement | \n      | 2    | 8            | 8          |                     
+------------------+---------+------+--------------+------------+    

This is it!

Enjoy your day!